The secret pattern hidden in your daily Sudoku – and it could help you solve puzzles more quickly

They baffle, delight and frustrate millions of people around the world every day.

But even the most dedicated Sudoku solver may never have noticed this secret pattern.

Mathematicians have discovered a powerful pattern known as the ‘Phistomefel Ring’ – and it’s hidden in every Sudoku ever created.

Best of all, puzzle experts say the pattern can help you solve the toughest challenges much faster.

This pattern means that the 16 squares around the central 3×3 ring will always contain the same numbers as the 2×2 squares in the corners.

Since this will always be the case with any legitimate Sudoku, you can use this rule to solve otherwise impossible problems.

Professor Sarah Hart, a mathematician at Birbeck, University of London and author of ‘Once Upon A Prime’, told MailOnline: ‘If you’re stuck in a devilish puzzle, knowing about some of these equivalent sets can sometimes be the key.’

Here’s how to use the pattern to your advantage in your next Sudoku.

A Sudoku is a puzzle with a 9×9 grid in which the numbers one to nine must be placed.

The catch is that each row, column, and 3×3 box must contain each of the numbers one through nine once, and only once.

Complying with these rules is what makes Sudokus challenging, but it also creates some mathematical patterns that we can exploit.

The Philstomefel ring is just one example of what mathematicians call the ‘Set Equivillence Theory’.

‘The basic idea is that in any Sudoku grid there are sets of cells that must contain the same set of numbers,’ says Professor Hart.

“Some of these are part of the definition. Each row contains the numbers 1 through 9 in a specific order, and so does each column, and so does each of the 3×3 blocks. So these are all equivalent sets.’

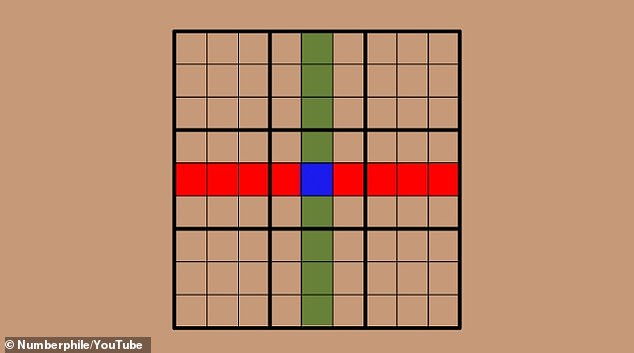
As explained in this video by YouTuber Numberphile, When we look at the central column and the central row of any Sudoku, we know that they must have the same set of numbers.

While we don’t necessarily know what order the numbers will be in, we do know that both will consist of the numbers one through nine.

In a Sudoku puzzle, each column, row and 3×3 box must contain the numbers one through nine, with each number appearing only once

Since the red and green sets must contain the same numbers (1-9), we know that the overlapping square must contribute the same number to each set. If we were to remove this blue square, the sets would still be identical

So far this may not seem groundbreaking, but things start to get interesting when we look at the points where the two equivalent sets overlap.

The central column and row have one square in common: the central square of the Sudoku.

Even if we don’t know what this square is, we know that it contributes the same number to both the vertical and horizontal sets.

If we remove this square, the same number is removed from both, so the sets are still identical.

For example, if the central square is the number ‘9’, then with this number removed, both sets would still contain the numbers one through eight in some order.

The point at which this starts to become useful is when we realize that there are larger equivalent sets with even more overlap.

Professor Hart says: ‘They are a few sets of cells containing the same numbers.

‘The Phistomefel ring is a very nice example of this, because it has a nice symmetry – the argument involved is just a little more complicated.’

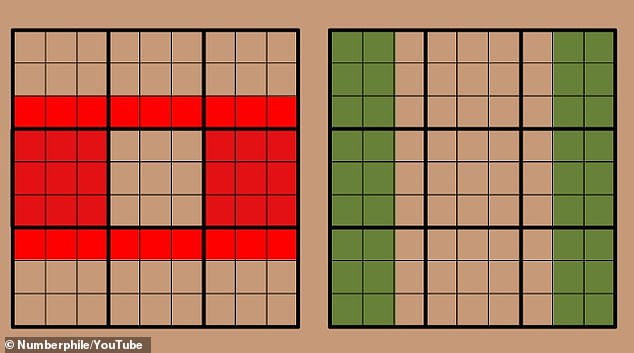
This rule called ‘Set Equivillence Theory’ can be applied to larger groups of squares, as long as they contain the same number of numbers (1-9 sets). In this diagram, both the red and green sets of squares contain the exact same numbers

Just as we did with the simple example, we can omit the overlapping squares and the remaining red and green squares will still contain identical sets of numbers

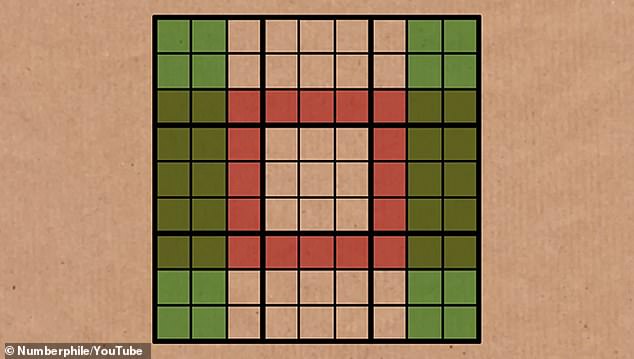
The Phistomefel ring starts with the two rightmost and leftmost columns of numbers.

These sets are then placed over the two 3×3 squares to the left and right of the central block and the rows directly above and below the central block.

You can see these more clearly illustrated in the diagram above.

We know from the rules of Sudoku that each of these sets must consist of four games of the numbers one through nine, arranged in a certain order.

As in the simple example, we also know that any space where the two sets overlap contributes to each the same number.

So by removing all the overlapping squares, we are left with a central ring of 16 squares and four 2×2 squares in each of the corners, which should contain the same numbers.

What makes this so useful is that it is true no matter how the numbers are arranged in the Sudoku.

This would be true even if the Sudoku did not use numbers, but rather consisted of emojis or letters. If the Sudoku is legit, the two sets will always contain the exact same things.

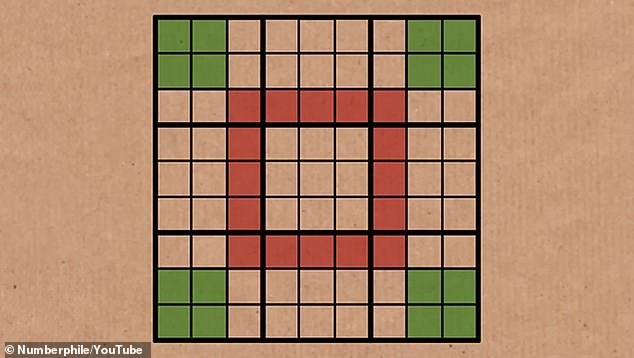
This leaves us with the Phistomefel Ring. Thanks to Set Equivalence Theory, we know that the 16 red squares in the center contain the same numbers as four 2×2 squares on the edges

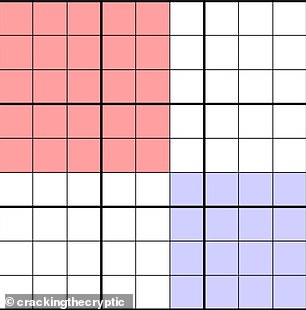
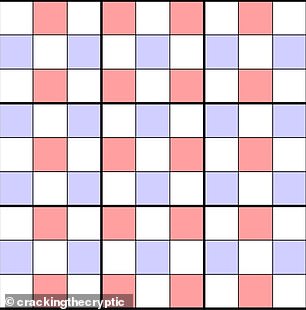
Using these rules, mathematicians and Sudoku constructors have identified other equivalent sets (photo). You can use these rules to solve any Sudoku puzzle quickly

“Mathematics is really about structures and patterns, which is why Sudokus are mathematical,” says Professor Hart.

The Phistomefel Ring isn’t even the only example of equivalent sets in Sudoku.

Mathematicians and puzzle designers have managed to discover a whole range of simple and complex equivalences.

Professor Hart says knowing these rules can be “a new weapon in the armory” for anyone who has trouble solving certain puzzles.

“These equivalent sets can be very useful for hard Sudokus where all the usual methods fail,” she added.

‘Just like in chess: the more openings, defenses or other tricky tactics you know, the more options you have to get out of trouble. ‘